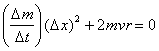The Analog-In, Digital-Out Universe
Edwin Eugene Klingman, klingman@geneman.com
Abstract
Is Reality Analog or Digital? Analog and digital mathematical treatments can be shown to be equivalent, so the answer does not lie in math but in physics. At root is the nature of particles and fields. The simplest possible physical model, one field, will be analyzed and physical experiments proposed to show an analog reality with digital consequences. There are implications for the view of reality currently associated with entanglement and violation of Bell's inequality.
_______________________________
Physics is a discipline that is approximately based on the following diagram:
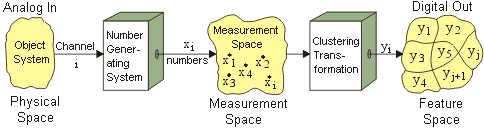
An
appropriately isolated object system, measured by an appropriate number
generator, produces a measurement space upon which clustering transformations
can be performed—by either neural or silicon networks—to create a feature space
that can be represented1 in either continuous or discrete formalisms
[appendix
A]. Steiglitz has
shown2 the equivalence of time-invariant
realizable analog filters and digital filters, so the theory of processing
analog signals and the theory of processing digital signals are equivalent.
Thus analog or digital reality questions can’t be answered mathematically—the
answer must be found in a physical universe. The simplest
possible universe would consist of one primordial field
.
Laws of
Physics: Physics should
never accept anything “outside time and space”, such as: God, a
mathematical universe, a multiverse, laws of physics, more than 4 dimensions. If
physics does not grant God legitimacy, it should reject all other appeals
to “the beyond”. If only a primordial field exists initially, then any law
of physics must derive from the field itself. Any operator 
applied
to the field can only be construed to represent the field interacting with
itself, so the symbolic Master equation representing this reality is
(1)
where the dot
represents interaction. Since one cannot derive physics from logic, we need
physical facts: Maxwell's energy 
and Einstein's energy ~
m. These suggest that 
is gravity, 
,
so 
[appendix B], and operator 
is a directional
derivative or tangent vector definable in any local coordinate
system on a manifold (including Calabi-Yau).
So we need math, but where does math come from? The -field
will support particles from which structures3
that generate integers are built, and, per Kronecker, man can produce the
rest of math—so we needn’t go outside the universe for math4 but can use math to solve the Master equation,
yielding 
hence 
. In
1953 Eugenio Calabi essentially asked if our Master equation was valid:
"Could there be gravity … even if space is a vacuum totally devoid of matter?"
He reasoned:
"…being non-linear, gravity can interact with itself and in the process
create mass”, and he conjectured, "curvature makes gravity without matter
possible". The Calabi-Yau manifold confirms5 our Master equation—based only on gravity —but his conjecture
was based on special geometry in which "time is frozen". Meaning
what? Newton's equation is time independent, but if we scale 
,
then 
and our Master field
equation is seen to be scale invariant (appendix C):
(2)
Nottale has
shown6 that the laws of scale can actually
take the place of the laws of motion: that is, scale invariance implies
motion invariance (
). This can be visualized
as:
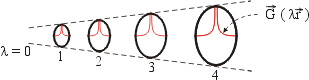
If scale
invariant is motion invariant, time has no obvious meaning. But action
orthogonal to a radial field vector can produce a vortex or cyclical
phenomenon in a region of space, introducing duration or cycle time.
So time appears when the -field symmetry breaks and
local oscillations, i.e. natural clocks, occur. The time dependent
phase occurs as symmetry breaking; thus formal time dependence4,8 of the solution 
yields
[appendix
D]:
|
|
 |
This equation
and two possible physical interpretations (shown) make sense only if both terms have a constant value,
call it 
, leading to the quantum
principle:
Classical Field equation - continuum physics (4)
Quantum Principle - physics of
observables (5)
This generalization
of Heisenberg's uncertainty principle also implies 
, Bohr's orbital
condition. Nottale says "it’s remarkable that the Heisenberg relations
are universal and independent of any particular measurement process" and
claims6 the relations imply a 'profound scale
dependence' of physical laws in the quantum domain. To see what scale is
associated with a local mass m, let 
and solve: 
.
For fixed mass, scale is min when 
is max (
,
the speed of light) so 
is the Compton
wavelength of the mass, the fundamental limitation on measuring the
position of a particle. FQXi asks: What do minimal length, time, or energy
imply? The Planck units of mass, length, and time yield an identity that implies
our Quantum Principle:
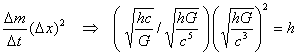(6)
( 
/ 
) ( 
)
FQXi also asked: How is time affected
by quantization? A change in time with respect to space, 
,
relates the mass gradient across the region, in units. So a
quantum gravitational gradient implies time dilation: (appendix E).
(7)
C-field physics: A classical field plus time dependence
leads to a quantum of action, , that enables a
fluctuation orthogonal to the field's radial symmetry, and introduces a rotational
aspect of the primordial field , viewed as a new field, 
.
Maxwell noted the -field analogy with the
magnetic field 
and wrote gravito-electro-magnetic
equations [GEM], which I’ve modified (appendix F) with 
and
(8)
where 
is
a dimensionless factor—derived8 from reasonable assumptions—that Tajmar
has also measured9. A Lorentz-like [
] force
provides 
, yielding natural antigravity
for an inflationary big bang. And, from (8), ignoring gravity, if 
,
then a change in the C-field circulation
(9)
produces a
Lenz-Law-like force that conserves linear momentum, solving Feynman’s mystery10. Angular momentum conservation is built in via and
C-field circulation is inextricably linked to local momentum since 
.
FQXi: Does
quantum nature imply the world can be modeled as digital computation? The
Automatic Theory of Physics states: “All axiomatized theories of physics
can be formally mapped into automatic machine representation.” A typical 3rd
order Feynman diagram1 quantum field theory kernel 
, shown below in
canonical form, maps the automata’s Next State-address into local
potential in physics.
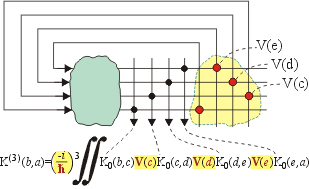
Approaches to Physics: Entities can count, so math evolves, set-theory arises, topological connections appear, distance induces metric on topology, repetition yields symmetry groups and physicists fall in love with such. Approaches to physics are metric and potential—physics is split into two mapping schemes: General Relativity and Quantum Mechanics. An example of a potential description is represented by the GEM differential equations shown below at left, the metric solution by the tensor at right: [abbrev. - appendix J]
=
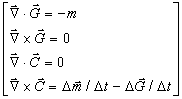
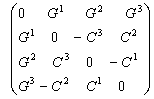
Their equivalence is seen in Sweetser’s view11 of metric and potential maps:
We can derive
relativity’s FLRW equation from GEM C-field equations, or we can derive the
gravito-magnetic equations from general relativity. The need for metric
maps arises only if tangent vector changes because the
manifold we’re moving on is in curved space. But both metric and potential
approaches have drawbacks—general relativity defines
5 only global mass, so “mass density is ill-defined in
general relativity”. Yet 
in (8) depends upon local
mass density. Other metric problems include: dark matter and energy; Second
Law entropy; ‘flat’ space; flat rotation curves; CMB ‘axis of evil’; etc.,
whereas problems for potentials derive from ‘point particles’ and from the fact
that scattering data fixes the strength and range of the nucleon potential,
but not its shape. As a result29:
The Lagrangian formulation provides a convenient technique for inventing new types of fields and investigating their properties.
The mathematical invention of fields offers no guarantee the fields physically exist. But it does allow the invention of Higgs, axions, dilatons, inflatons, anyons, instantons, WIMPs , sphalerons, gluons26, and SUSY particles. None of these have ever been seen. [appendix H]
Particles and Fields: Physicists also form ‘effective’ potential fields from statistical combinations of particles and then they treat these fields as ‘real’:
• Hartree-Fock28: atomic electrons averaged; viewed as a field.
• Dark matter particles: viewed as a distributed field.
• Einstein photons: viewed as Maxwell’s electric field.
• Yukawa’s pion exchange12: viewed as the strong field.
The ‘field’ serves as an approximation that allows an unsolvable N-body problem to be solved as 1-body in a potential. Yet after 80 years of pion exchange, Wilczek—father of QCD— says12 that Yukawa pion exchange fails at hard core distances. With all of these choices of representation for the many models, it’s no wonder physicists are confused about particles and fields—both because Lagrangian techniques allow fields to be invented freely, and because particles and fields are interchangeable in QED [but see Appendix I].
Particles
from a field: How can
we derive real particles, distinguishable from a real field? We
need a final assumption: that the curvature of space is limited. Without
a limit, space can curve in upon itself to produce infinitely dense mass points—limits
prevent this. Electrons and quarks8,21 appear as limits to the curvature of ,
and black holes as limits to the curvature of .
Limiting phenomena are defined by mass, charge, and spin:
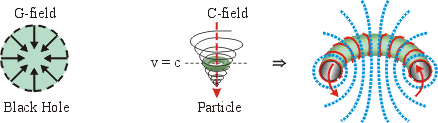
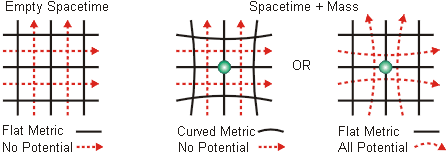
When the C-field reaches the limit of curvature, the vortex wall is a mass current loop, inducing a secondary C-field circulation and converting to a torus topology, a Calabi-Yau manifold5 (Kähler, Ricci-flat with Chern class 0) supporting spin ½, containing SU(n) symmetry, and regarded as a solution to Einstein’s differential equations.
Are particles and fields interchangeable, as assumed in standard models, or does a field—a fundamental continuum—condense into discrete particles when curvature limits are reached? Yang-Mills C-field vortices8 condense to Majorana neutrinos, electrons, and quarks, and supply the mechanisms of weak and strong forces—all derived from C-field.
Local Reality: Are these neutrinos,
electrons, and quarks locally real, or are they superpositions of
states? deBroglie, Schrödinger, Einstein, and Dirac preferred a ‘particle
plus pilot wave’ view—compatible with two-slit experiments and entanglement
phenomena. Both electrons and photons possess momentum, so the C-field
circulation 
applies to both and implies
a real particle with a Lenz-law-like pilot wave:
|
Particle plus pilot wave:
|
 |
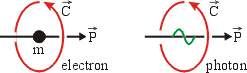The
parameters for particle plus pilot wave—momentum 
and field —
provide the standard free particle solution to Schrödinger’s equation and
support Bohr’s principle of particle/wave complementarity. Collapse of the
wave function is not part of QM—it’s an add-on7. Although the consensus among physicists seems to be
that local reality doesn't exist, recent Physical Review Letters papers13, 25 state the factual truth:
"…no experiment ever closed both the locality and the detector-efficiency loopholes to conclusively rule out local hidden variable theories." [and] “A finite amount of data cannot conclusively demonstrate entanglement.”
Momentum-induced
C-field circulation, as local hidden variable, has never been ruled out—or even
explored. Superposition of states is a consensus interpretation,
not a physical fact. Collapsing wave functions imply to some that particles
exist as ‘probability waves’ when not observed. But analog inputs applied to
classical electron orbits—unlike jumps associated with quantum inputs—should
'smear' the orbit—exactly what is found. And interpretation as a ‘superposition
of states’ rather than a 'smeared orbit' is challenged by recent14 non-dispersing Bohr orbits in which the electron
behaves as a localized particle orbiting the nucleus in a classical orbit. This
makes sense for analog disturbances applied to locally real particles with
circulating C-field proportional to momentum:. Non-dispersing
Bohr orbits argue for real particles and analog fields.
While entanglement
has no known mechanism
(spooky being the universal term of reference), in GEM, the C-field is
the physical medium of entanglement with implications for locality and
reality. The quantum mechanics of a particle with mass m and charge q in an
electromagnetic field, 
and 
, is
formulated in terms of potential vector A (despite A being indeterminate
within gauge invariance), and the Hamiltonian is based on momentum 
instead
of simply . But whereas quantum
mechanics of free particles and atomic electrons are well represented by we
find 
has dependent
on local mass density. And unlike free particles, photons encountering beam
splitters can experience variations in local mass density.
Zeilinger explains15 Bell's inequality based upon properties of sets of twins with different hair and eye colors and heights [appendix G]. He shows how statistical inequalities are derived based on these properties, and concludes that experiments showing violation of Bell's inequality imply that such properties do not exist until measured. This radical conclusion is the basis of today's rejection of local realism.
But there is a simple alternative to his analysis. If one or more twins dyes his hair enroute, Bell's inequality will be violated, yet local realism exists. Solar neutrinos change enroute from the sun; why not photons? A GEM explanation is compatible with such entanglement. Many physicists are enamoured of entanglement’s 'spookiness' and relatively unbothered by non-local non-real reality, but if local properties can change enroute, their arguments fail. If Zeilinger’s explanation of Bell’s inequality is valid, GEM is compatible with local realism.
GEM physics supports the local realism that the great physicists insisted upon.
C-field Cosmology: If the entire universe evolves from our Master equation, we need
not only particles but cosmology. Penrose claims16 big bang entropy—while scale invariant—must
be minimal due to ever-increasing entropy. But all of general
relativity’s homogenous FLRW models with high entropy ‘dust’ fail this
criterion. Yet most field-energy-mass of our G field is near the 
singularity,
thereby achieving the required minimal entropy:
The universe’s expansion is in striking accordance with Einstein's general theory of relativity, “but only if two somewhat unexpected ingredients are incorporated…dark matter and dark energy." We can derive17 the FLRW equation at left from (8) and compare:
(10)
The general
relativity version at right implies that C-field energy is Einstein’s
cosmological constant 
, responsible for late
inflation. If only 5% of C-field energy condenses to particles then 95% of
C-field energy of the universe remains uncondensed. Directed
entities 
, 
,
add and subtract: 
is inflationary, hence dark
energy; but 
augments gravity, hence dark
matter. But 
is equally distributed in
all directions, while is directed to the
‘center’ of the mass distribution. At any location approximately ¼ of is
additive (dark matter) while ¾ is subtractive (dark energy) as shown below:
|
100% = C-field universe, partitioned as: 5% = condensed
95% = uncondensed
23% = 'dark matter' 72% = 'dark energy' |
|
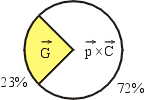
Is the dark matter comprising most of the Universe a field or particles? Many different particles have been proposed as dark matter, but all of them should become trapped in the Sun’s gravity well18. If dark matter is a continuous field the sun should show it—thus an experimental test should be able to distinguish an analog C-field from particulate (digital) dark matter.
“Gravity at large distances poses some of the most difficult puzzles in contemporary gravitational physics…”19
These puzzles
include the cosmological constant, the nature of dark matter, flyby
anomalies, the Pioneer anomaly and Rubin’s flat rotation curves
seen in galaxies and clusters, as well as the CMB axis of evil. All
are unexplained by general relativity. The C-field qualitatively
explains them and now (19
Nov 2010) Grumiller provides19 numbers needed for quantitative analysis. With natural
units 
and 
, he
reports the scale of observed anomalous accelerations is 
: with spiral
galaxies~
; Galaxy-Sun ~;
Sun-Pioneer spacecraft ~
; …while Sun-Mercury
and Earth-satellite may be larger.
If C-field
energy 
in (10) is identified as
the cosmological constant, then says that 
—almost
exactly the acceleration needed to explain these phenomena via 
.
Grumiller: “It is a challenging open issue to understand precisely what
determines the scale of 
.” While general
relativity can’t handle mass density the C-field depends on local mass
density via in (8) and this can
explain variation in the scale of .
Finally the LHC has surprised physicists/cosmologists20 that the early universe was a ‘perfect fluid’, not an ‘explosion of gases' that is the basis of all current theories. Our Master equation describes4 a perfect fluid, a G-C-field yielding the most complete explanation of our universe for all known particles and cosmological phenomena—that is compatible with SU(n), Yang-Mills, Calabi-Yau, 3D space and time, and local realism.
The following physical experiments should establish the analog-digital nature of reality:
Measurement of the C-field to demonstrate its reality
Non-dispersing electron orbits demonstrate the digital nature of particles
A solar test of ‘dark matter’ to demonstrate the analog reality of the C-field
Summary: Today relativity and quantum mechanics can’t explain the known particles of physics. GEM theory does and predicts no new particles, based on a particle plus pilot wave model that is QM-compatible. Nor can general relativity and quantum mechanics handle serious problems such as the following, explained21 in Physics of the Chromodynamics War.
• Why does QED fail to get within 4% of the proton radius (in muonic hydrogen)?
• Why is the core of the neutron negative? (QCD predicts positive).
• Why are there three particle families?
• Why does the
decay into 3
?
• Why do 6 deuterium quarks not collapse to a sphere, but maintain ‘cigar’ shape?
• Why does an electron exist in a non-dispersing (classical) orbit?
• Why can’t QED derive the ‘fine structure constant’ – GEM can.
• What explains relative mass order of: electron, up, down quarks?
• Why are Halo neutrons stable beyond the range of the strong force?
Again and again GR fails to cope with cosmological phenomena because of its geometrical—essentially static—treatment of curvature of space, well adapted to radial gravity fields. Einstein tried and failed27 to solve the simplest C-field dipole—the gravito-magneto-static problem, and (aside from ‘frame dragging’) few have ventured here. General Relativity is beautiful, but inappropriate for Yang-Mills/Calabi-Yau instances of self-interacting C-fields, failing to explain Rubin’s flat rotation curves, dark matter, dark energy, and CMB axes, while the actual ‘flat’ curvature of our universe limits G-curvature issues to black holes and neutron stars, and, even then, rotating bodies will induce the C-fields seen in jets.
If Tajmar’s measurement of the C-field and my calculations are correct, the C-field explains physics mysteries via a real, not an invented, field. And not just one mystery, but dozens of mysteries. Fields and particles are not interchangeable, as is the case in quantum field theory. C-field vortex bosons induce local condensation of real massive left-handed Majorana neutrinos. Yet this cosmological and particle physics explanation for current physics is far simpler than many physicists wish it to be because, as Robert Godwin says22
One begins by abstracting from concrete existence,
and ends by attributing concreteness to the abstraction.
Perhaps due to lack of new particle physics for 40 years—many physicists have moved deep into abstraction and away from reality, attributing reality to abstract mathematics, making acceptance of a simpler physical theory that much harder. But failure of Higgs, SUSY, dark matter particles, etc to appear might eventually force reconceptualization on physics.
And the cosmological ‘fly-by’ mysteries aren’t going away…
Assuming a primordial field—and nothing else—yields the major physics equations and conditions, with low initial entropy, and explains all known particles8 sans Higgs. Quantum conditions—Bohr’s orbital momentum and generalized Heisenberg principle—derive from a continuous field, implying an analog and digital world. A primordial (gravity) field, initially self-subject to a Master equation, whose scale invariance implies motion invariance until symmetry breaks, forms vortex phenomena that lead to the evolution of the Universe as we know it. A continuous universe evolves to discrete reality, where quantum conditions carve up the continuum, such that analog inputs occasion digital outputs or threshold crossings. Finally, the real field supports particles with properties compatible with local realism, and explains how Bell's inequality is violated with no consequence for local realism.
Physical reality depends on continuous fields.
Informed reality depends upon the existence of thresholds, or universal constants.
Beauty is truth,
truth beauty, and
that is all
Ye know on earth,
/ | | \ and all ye need to know.
space time distance mass Keats
References
1 Klingman, The Automatic Theory of Physics, 2010 ISBN 978-0-979-17652-4
2 Steiglitz, “Information and Control”, Vol. 8, No. 5, (1965), p. 455-467
3 Klingman, Microprocessor Systems Design, 1977 ISBN 0-13-581413-8
4 Klingman, Gene Man's World, 2008 ISBN: 978-0-9791765-5-5
5 Yau, The Shape of Inner Space, 2010 ISBN 978-0-465-02023-2
6 Nottale, Theory of Scale Relativity, 1991 Intl. J. of Mod. Physics A, Vol 7,#20
7 Gribbin, In Search of the Multiverse, 2009 ISBN: 978-0-470-61352-8
8 Klingman, The Chromodynamics War, 2009 ISBN: 978-0-979-17657-9
9
Tajmar, et al, http://lanl.arxiv.org/ftp/gr-qc/papers/0603/0603033.pdf
‘Experimental Detection of the Gravitomagnetic London Moment’
10 Feynman, The Character of Physical Law, 1965 Lib of Congress 67-14527
11
Sweetser, ‘Doing
Physics with Quaternions’,
http://world.std.com/~sweetser/quaternions/qindex/qindex.html
12 Wilczek, ‘Hard-core Revelations’, Nature, Vol 445 11 Jan 2007 p.156
13 Se-Wan, et al, ‘Loophole Free Bell Test…’, Phys Rev Lett 105, 170404, 22 Oct 2010
14 Maeda et al, ‘Non-dispersing Bohr Wave Packets’, PRL 102, 103001, 13 Mar 2009
15 Zeilinger, Dance of the Photons, 2010 ISBN 978-0-374-23966-4
16 Penrose, Cycles of Time 2010 ISBN 978-0-224-08036-1
17 Klingman, The Gene Man Theory, 2007 ISBN 978-0-979-17654-8
18 ‘Dark Matter may be building up inside the Sun’, http://www.wired.com/wiredscience/2010/07/dark-matter-sun/
19 Grumiller, ‘Model for Gravity at Large Distances’, PRL 105, 211303, 19 Nov 2010
20 ‘How the universe evolved from a liquid’: http://www.telegraph.co.uk/science/science-news/8148525/How-the-universe-evolved-from-a-liquid.html
21 Klingman, Physics of the Chromodynamics War, 2011
22 Godwin, One Cosmos Under God, 2004, ISBN 1-55778-836-7
23 Klingman, fqxi essay ‘Fundamental Physics of Consciousness’ http://www.fqxi.org/community/forum/topic/essay-download/561/__details/Klingman_Ultimatelypossible_1.pdf
24 Waltz and Buchanon, ‘Automating Science’, Science Vol 324 3 Apr 2009
25 Blume-Kohout et al, ‘Entanglement Verification…’, PRL 105, 170501 22 Oct 2010
26 Voloshin, ‘Testing Chiral Magnetic…’, PRL 105, 172301, 22 Oct 2010
27 Pais, Subtle is the Lord: Albert Einstein, 1982 ISBN 978-0-19-280672-7
28 Fischer, The Hartree-Fock Method for Atoms, 1977 ISBN 0-471-25990-X
29 Goldstein, Classical Mechanics, 1959 Lib of Congress 50-7669
Appendices
Appendix A: The Derivation of Theories of Physics from Numbers: The Automatic Theory of Physics describes how continuous functions can be mapped onto a feature set derived from numerical measurements as represented below:
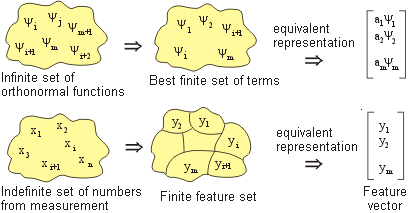
The following five questions are answered in detail:
• Q1 How to reduce an indefinite number of measurements to finite number of features.
• Q2 What is the criterion for “best” feature set?
• Q3 How can we obtain the best feature set?
• Q4 How will we describe the dynamical behavior of the object?
• Q5 What is the best physical theory?
Appendix B: Derivation of Newton’s equation
from the Master equation: Maxwell: energy and Einstein:
energy ~ m, suggesting 
.
If is
gravity, , then energy is negative,
and formal equivalence to Newton’s gravitational equation: , implies that is
the directional derivative.
Appendix C: Demonstration that the Master
equation is scale invariant: The field configuration determined by solving
the Master field equation is 
. If we rescale 
we
obtain (for 
) then 
Since 
the
solution field configuration is scale invariant
according to Wikipedia’s
requirement: 
. But we’ve yet to show
that our field equation is scale invariant. We do so by replacing the original
field 
with the rescaled field 
in
the equation 
.
Scaled: 
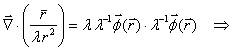
Appendix D: Derivation of Quantum Principle
from the Master equation: The Master equation solution is hence
. The formal change with
respect to time 
, hence 
.
This yields 
which
is only generally true if both sides are constant, , leading to the
Quantum Principle and Bohr’s orbital condition.
Appendix E: Time dilation derived from the Master equation:
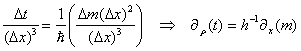
Appendix F: Summary of the GEM equations derived from the Master equation: The G and C field equation’s are Yang-Mills self-interacting as required for strong field physics.
+
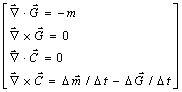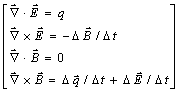
Appendix G: Anton Zeilinger's (Dance of the Photons) develops a translation of Bell's inequality for non-physicists:
Appendix H: How long can this go on? AT&T analyzed 'bugs' in software: Many bugs are first found in new software (the model) but as the search continues time between bugs grows exponentially—providing an estimate of the bugs remaining and hence the validity of the model. And the longer colliders run without finding the postulated particles, the less likely that the current models are valid.
Appendix I: QED’s vaunted 10 place accuracy is
now 1 place accuracy: the QED proton radius is off by 4% and vacuum energy
is off by 
. These facts are more
serious than most physicists have yet realized. And QED requires a
Higgs field, still not seen.
Appendix J: Abbreviations of common terms:
CMB – Cosmic Microwave Background FLRW – Friedericson, LeMaitre, Robertson, Walker
GEM – Gravito Electro Magnetics GR – General Relativity
LHC – Large Hadron Collider CERN QFT – Quantum Field Theory
QCD – Quantum Chromodynamics QED – Quantum Electrodynamics
QM – Quantum Mechanics SM – Standard Model of Particle Physics
SUSY – SuperSymmetry